Conformal Prediction: A light introduction

In the ever-evolving world of machine learning, where algorithms are tasked with making predictions about complex systems, the ability to accurately quantify uncertainty is paramount. This is where conformal prediction (CP) steps in, offering a powerful framework for building trust and reliability in our models.

What is Conformal Prediction?

Conformal prediction is a relatively new technique that goes beyond the traditional point predictions generated by algorithms. Instead, it focuses on constructing prediction sets, which are guaranteed to contain the true value with a user-specified confidence level, even for unseen data. This guarantee holds true regardless of the underlying model complexity or data distribution, making CP a versatile tool for various applications.

Main Idea

The key idea behind conformal prediction is to estimate a prediction region or set that will contain the true label with a certain probability, instead of outputting a single predicted value. This is done by:

Training a machine learning model on a subset of the available data, called the "proper training set".
Applying the trained model to the remaining data, known as the "calibration set", to produce predictions along with a measure of confidence (like a probability estimate).
Ordering the calibration examples by their confidence scores. Less confident predictions should fall lower in the ranking.
Gradually going down the ranked list and recording the least confident rank/index at which each possible label first appears. This forms a "nonconformity score".
For a new unlabeled example, the model produces a prediction and confidence score, which determines where it would be inserted into the ranked calibration set.
Looking up the nonconformity scores recorded earlier to construct a prediction set that contains all labels that meet the desired confidence level based on the ranking.

This shows some example code

from sklearn.ensemble import RandomForestClassifier
from nonconformist.icp import IcpClassifier
from nonconformist.nc import NcFactory

# Train a random forest model on the proper training set
rf = RandomForestClassifier()
rf.fit(X_train, y_train)

# Create a nonconformity scorer using the trained RF  
nc = NcFactory.create_nc(rf.predict_proba)

# Create the conformal predictor wrapping the RF model
icp = IcpClassifier(nc)

# Calibrate the ICP on the calibration set
icp.fit(X_cal, y_cal)  

# Make conformal predictions on new data
prediction = icp.predict(X_new, significance=0.1)

print(prediction)
# Example output: [0, 1] (with 90% confidence of containing true class)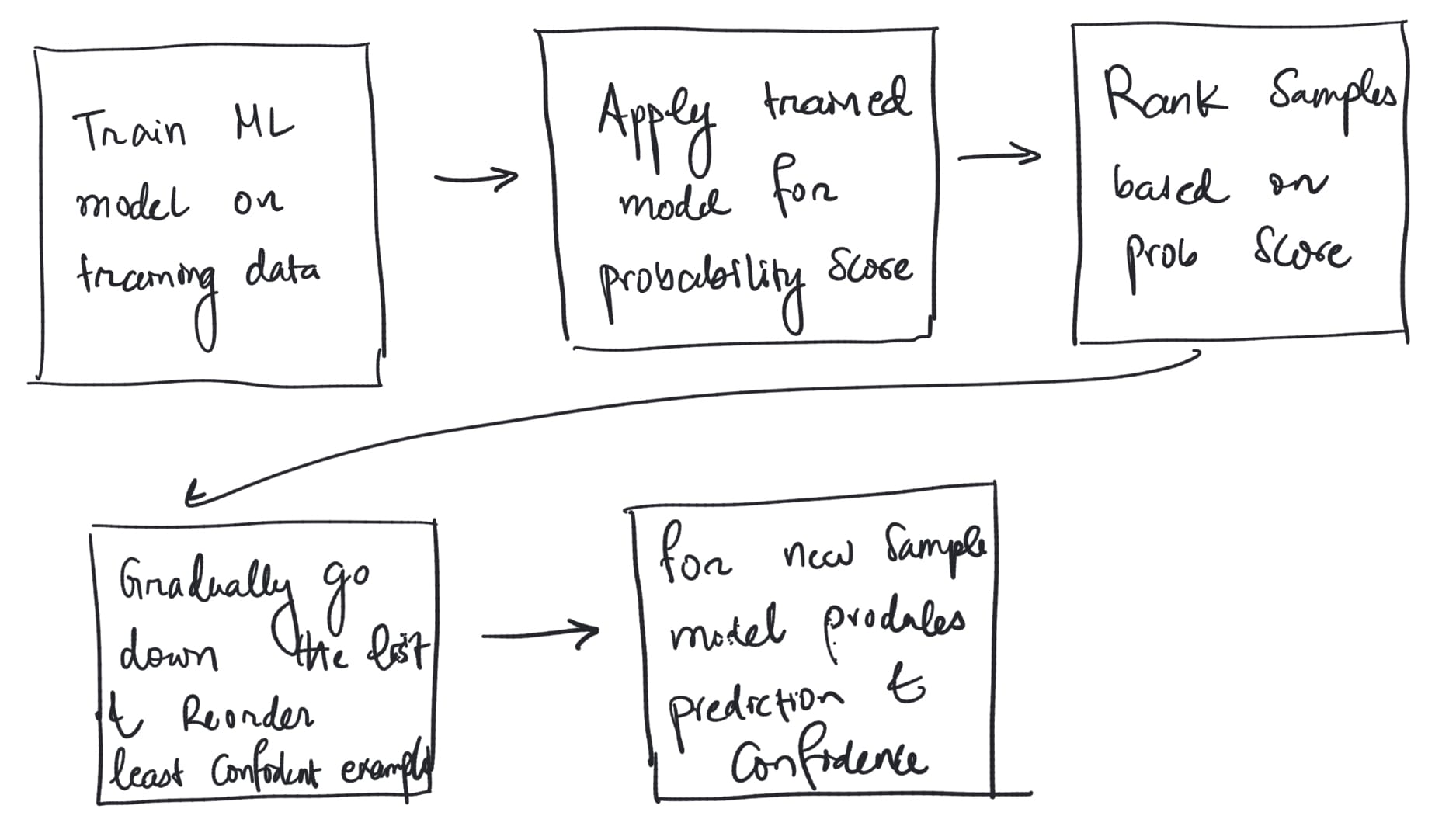

The Birth of a New Idea:

The roots of CP can be traced back to the mid-1990s, where Vladimir Vovk and his colleagues at Royal Holloway, University of College London, sparked the initial discussions. Their work, culminating in the definitive reference by Vovk et al. (2005), laid the foundation for this innovative approach.

Gaining Traction in the Statistical Community:

While Vovk and his collaborators continued their research on CP, its influence within the statistics community remained limited for some time. It wasn't until the mid-2010s, through the efforts of Larry Wasserman and his colleagues at Carnegie Mellon University, that CP gained traction in this domain. Their collaborations, including the work of Jing Lei, further solidified the theoretical framework presented in Lei et al. (2018) and Tibshirani et al. (2019).

A Recent Explosion of Interest:

In recent years, CP has experienced a surge in popularity within the machine learning community. This surge can be attributed to several factors, including:

Addressing model uncertainty: CP offers a robust way to quantify uncertainty, which is crucial for building reliable and trustworthy machine learning models.
Model-agnostic: Unlike other uncertainty quantification methods that rely on specific model assumptions, CP is universally applicable to any prediction algorithm.
Strong theoretical guarantees: The finite-sample coverage properties of CP provide strong guarantees on the accuracy of predicted intervals, even with limited data.

Exploring the Frontiers:

The field of conformal prediction is still rapidly evolving, with researchers actively exploring new frontiers. A recent comprehensive overview by Angelopoulos and Bates (2023) provides a glimpse into the current trends and future directions of this exciting field.

Conclusion:

Conformal prediction is a revolutionary technique for quantifying uncertainty in machine learning predictions. With its strong theoretical foundations, flexibility, and recent surge in popularity, CP promises to play a pivotal role in building reliable and trustworthy AI systems in the years to come.

Additional Resources:

Angelopoulos, N., & Bates, S. (2023). Conformal Prediction for Reliable Machine Learning. Springer.
Lei, J., Wasserman, L., & others. (2018). Distribution-free prediction sets. Journal of Machine Learning Research, 19(1), 1499-1532.
Tibshirani, R., Zhang, J., & others. (2019). Conformal prediction for low-rank matrix regression. Journal of Machine Learning Research, 20(1), 3396-3440.
Vovk, V., Gammerman, A., & Shafer, G. (2005). Algorithmic Learning in a Random World. Springer.

Python Library for conformal prediction