Understanding Batch Normalization: Enhancements and Limitations

Batch Normalization (BN) has become a cornerstone technique in deep learning since its introduction by Sergey Ioffe and Christian Szegedy in 2015. Designed to accelerate deep network training, it has evolved over the years, addressing both its inherent limitations and adapting to new challenges in the field. This blog post delves into the workings of BN, its advantages and limitations, and the improvements made in recent years.

How Batch Normalization Works

Batch Normalization fundamentally addresses the issue of internal covariate shift – the problem where the distribution of each layer's inputs changes during training, slowing down the training process. BN normalizes the inputs of each layer so that they have a mean of zero and a variance of one. This is achieved through the following steps:

Standardizing Inputs: For a given layer, BN standardizes the inputs over the mini-batch. If we consider (x) as the input, the mean ($\mu_B$) and variance ($\sigma_B^2$) are computed for the mini-batch (B). The standardized input, ($\hat{x}$), is calculated as:$[
\hat{x} = \frac{x - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}
]$where ($\epsilon$) is a small constant added for numerical stability.
Scaling and Shifting: Post standardization, BN applies two trainable parameters, ($\gamma$) (scaling) and ($\beta$) (shifting), to restore the representation power of the network:$[
y = \gamma\hat{x} + \beta
]$Here, ($y$) is the output that is passed to the next layer.

Advantages in Deep Neural Network Training

The integration of BN into deep neural networks has brought several advantages:

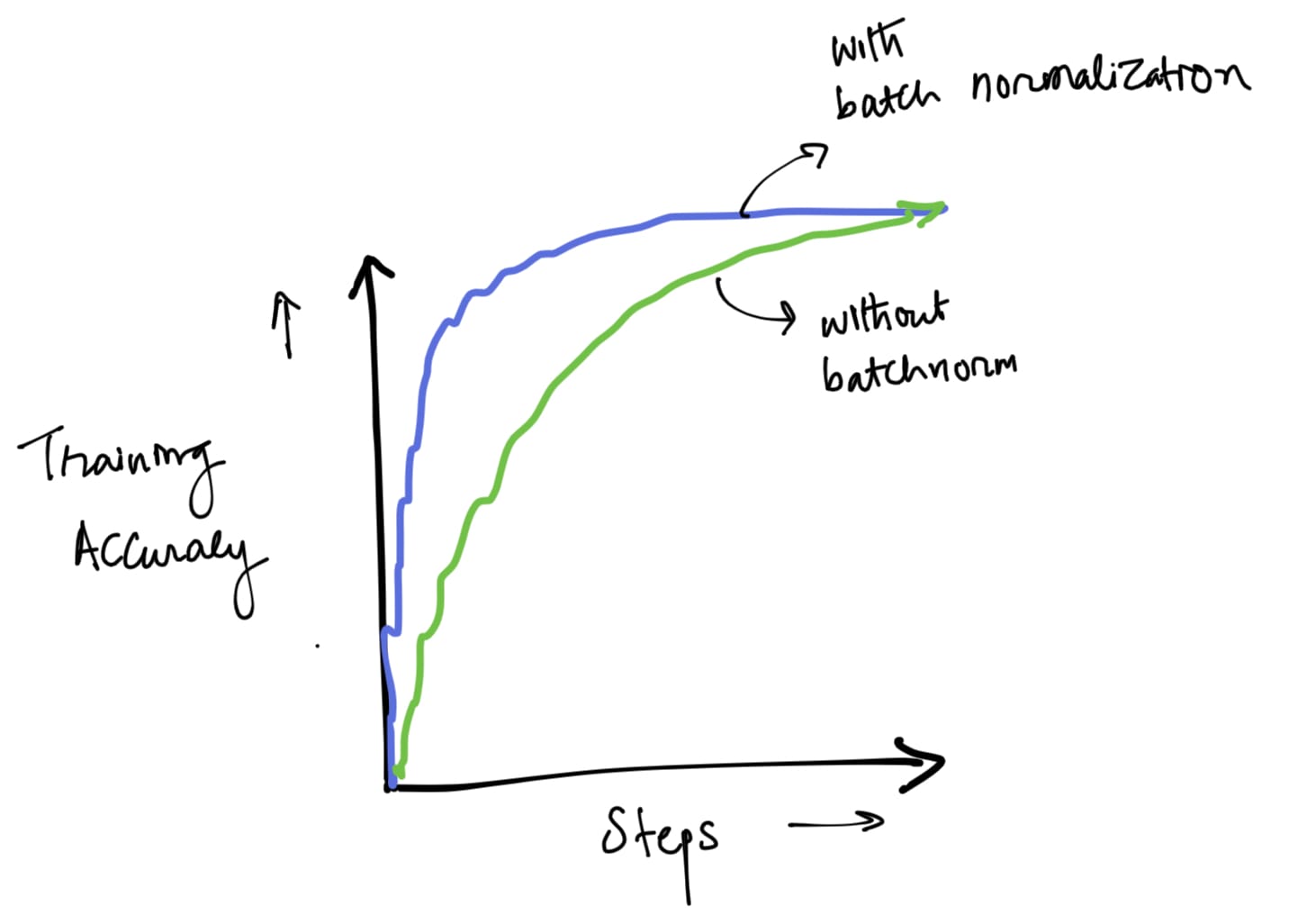
Improves Training Speed: By normalizing the inputs, BN allows for higher learning rates, accelerating the training process.
Reduces Internal Covariate Shift: It stabilizes the learning process by ensuring that each layer's inputs have a more stable distribution.
Lessens the Need for Careful Weight Initialization: With BN, networks become less sensitive to the initial starting weights.
Acts as a Regularizer: BN introduces a slight noise in the training process, which can reduce overfitting, acting similarly to a regularizer.

Central Limitations of Batch Normalization

Despite its benefits, BN is not without limitations:

Dependency on Mini-Batch Size: BN's effectiveness diminishes with smaller batch sizes, as the estimate of the mean and variance become less accurate.
Incompatibility with Recurrent Neural Networks (RNNs): BN’s reliance on mini-batch statistics makes it challenging to apply in RNNs, where sequential data and varying time steps are involved.
Normalization Discrepancy During Training and Inference: The differing behavior of BN during training (where batch statistics are used) and inference (where population statistics are used) can lead to performance degradation.

Implementation of Batch Normalization in Python

Implementing Batch Normalization in pure Python involves writing code to perform the standardization and learnable shift/scale operations on a batch of input data. It's important to note that this implementation is for educational purposes and will not be as efficient as optimized libraries like TensorFlow or PyTorch.

import numpy as np

class BatchNormalization:
    def __init__(self, epsilon=1e-5, momentum=0.9):
        self.epsilon = epsilon
        self.momentum = momentum
        self.gamma = None
        self.beta = None
        self.running_mean = None
        self.running_var = None

    def fit(self, X):
        # Initialize gamma and beta if they are not set
        if self.gamma is None:
            self.gamma = np.ones(X.shape[1])
            self.beta = np.zeros(X.shape[1])
            self.running_mean = np.zeros(X.shape[1])
            self.running_var = np.zeros(X.shape[1])

        # Calculate mean and variance for the batch
        batch_mean = np.mean(X, axis=0)
        batch_var = np.var(X, axis=0)

        # Update running mean and variance
        self.running_mean = self.momentum * self.running_mean + (1 - self.momentum) * batch_mean
        self.running_var = self.momentum * self.running_var + (1 - self.momentum) * batch_var

        # Normalize the batch and scale and shift
        X_hat = (X - batch_mean) / np.sqrt(batch_var + self.epsilon)
        out = self.gamma * X_hat + self.beta

        return out

    def transform(self, X):
        # Normalize using running mean and variance
        X_hat = (X - self.running_mean) / np.sqrt(self.running_var + self.epsilon)
        out = self.gamma * X_hat + self.beta

        return out

This implementation has the following components:

Initialization: gamma and beta are initialized to ones and zeros, respectively. running_mean and running_var are used to keep track of statistics across batches.
Fitting: During the training (fit method), it computes the mean and variance of the batch, updates the running mean and variance, normalizes the batch, and then applies the learnable gamma and beta.
Transformation: The transform method is used during inference. It normalizes the data using the running mean and variance calculated during training.

Recent Improvements to Batch Normalization

To address these limitations, several enhancements have been proposed:

Layer Normalization (LN): LN normalizes across the features instead of the batch dimension, making it more suitable for small batches and RNNs.
Instance Normalization (IN): Mainly used in style transfer networks, IN normalizes across each instance in the batch independently.
Group Normalization (GN): GN divides the channels into groups and normalizes the features within each group, which is effective for small batch sizes.
Adaptive Normalization Techniques: These methods adaptively adjust the normalization parameters during training for better stability and performance.

Conclusion

Batch Normalization marked a significant advance in training deep neural networks, primarily by addressing the issue of internal covariate shift. While it brought substantial improvements in training speed and stability, its limitations necessitated the development of alternative normalization techniques. These enhancements have expanded the applicability of normalization methods across various network architectures and training scenarios, reflecting the dynamic and evolving nature of the field of deep learning. As the field continues to grow, further innovations in normalization techniques are expected, enhancing the efficiency and effectiveness of deep learning models.

References