Linear regression and linear mixed-effects models are two statistical methods often used in data analysis, but they serve different purposes and have distinct features.

Linear Regression: It's a basic form of statistical analysis, ideal for examining the relationship between two variables. It assumes independence of observations and homogeneity of variance across data points. Linear regression is simple and straightforward but may not be suitable for complex datasets, especially when dealing with longitudinal data or data with inherent variability.

Linear Mixed-Effects Models: These models offer a more sophisticated approach, ideal for complex, hierarchical, or longitudinal data. They can handle variability both within and between groups, accounting for random effects. This makes them suitable for datasets where observations are not independent, such as repeated measures from the same subjects over time.

In summary, while linear regression is useful for simpler, independent datasets, linear mixed-effects models are more adept at handling complex, interrelated data, making them a better choice for nuanced analyses.

Linear Mixed Effect Model

Linear Mixed-Effects Models (LMM) are advanced statistical tools used for analyzing data where observations are not independent. These models are particularly useful in handling data with multiple layers of random effects, such as measurements taken from different subjects over time or clustered data like students within schools.

LMMs incorporate both fixed effects, which are consistent across all observations (like the overall effect of a treatment), and random effects, which vary (like individual differences). This dual approach allows for more accurate predictions and inferences, especially in complex datasets.

The flexibility of LMMs in modeling different levels of variability is a key advantage. They can account for both within-group and between-group variance, making them ideal for longitudinal studies or hierarchical data structures.

Statistically, LMMs extend the general linear model by including random effects, resulting in mixed linear equations. The estimation of these models often involves advanced techniques like Restricted Maximum Likelihood (REML) or Bayesian methods, which can handle the complexity of the mixed-effects structure.

In practice, LMMs require careful consideration of the random effects structure and the correlation within groups. Mis-specification of these elements can lead to incorrect conclusions. Hence, expertise in both the statistical methodology and the subject matter is crucial for the effective application of LMMs.

For a more detailed and technical exploration of Linear Mixed-Effects Models, you might want to delve into specialized statistical literature or comprehensive resources like academic articles.

Here's an example of how you can run a linear mixed-effects model in R using the lme4 package. We'll use the sleepstudy dataset, which is built into the package. This dataset records the reaction times of subjects across several days of sleep deprivation.

install.packages("lme4")
library(lme4)

data("sleepstudy", package = "lme4")

# Fit the linear mixed-effects model
model <- lmer(Reaction ~ Days + (1 | Subject), data = sleepstudy)

# Display the summary of the model
summary(model)

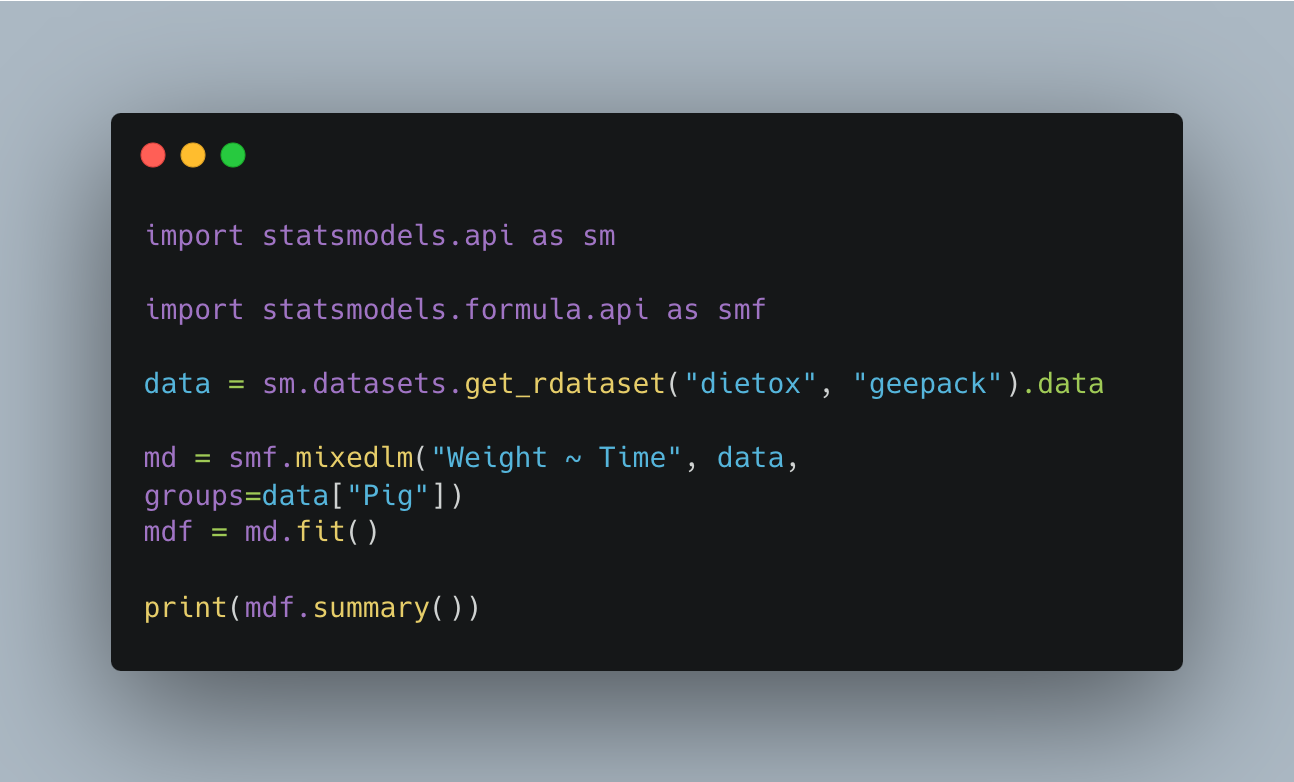
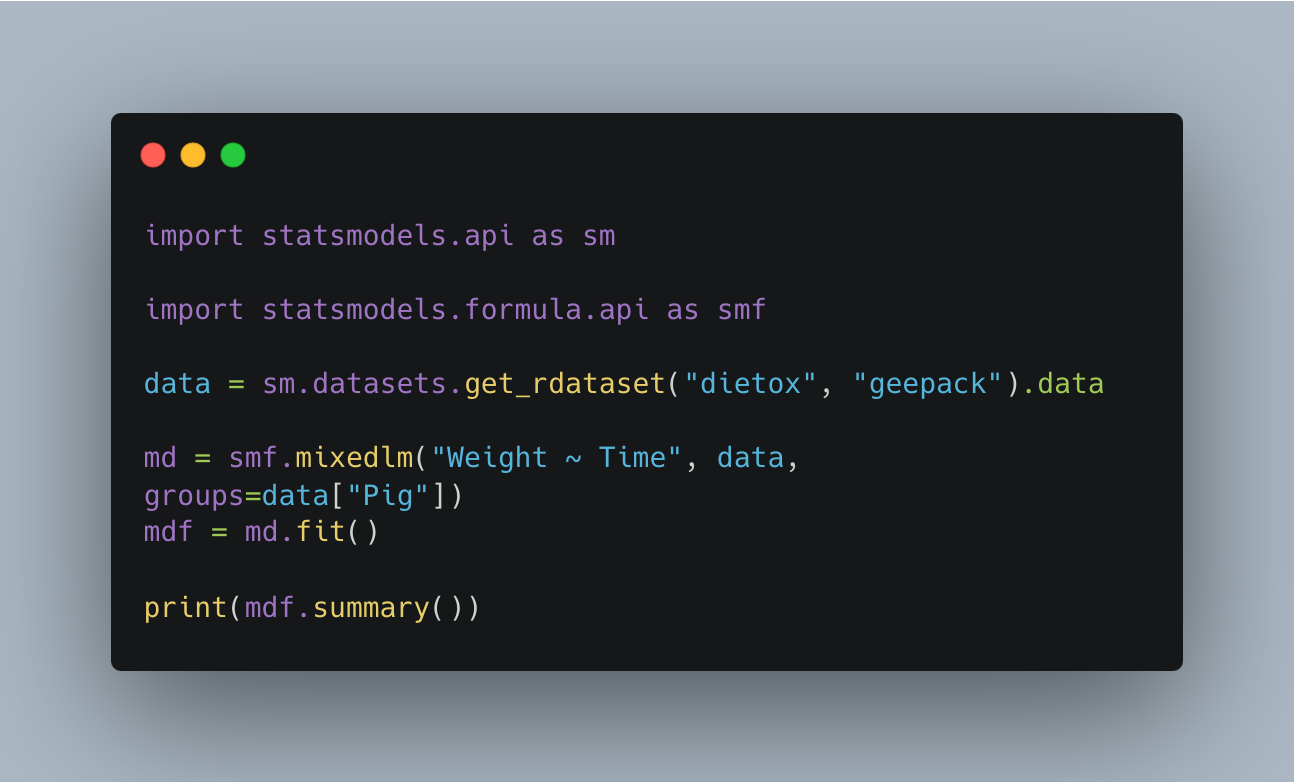
How to run linear mixed effect model in Python

Python's statsmodels package empowers you to delve into the intricacies of hierarchical data structures with linear mixed effects models (LMMs). Here's a glimpse into its capabilities